
Динамика – это раздел механики, изучающий причины механических движений тел. Любое движение может быть представлено суммой прямолинейных и вращательных движений, поэтому законы динамики изучаются в первую очередь для них. Рассмотрим динамику вращательного движения твердого тела.
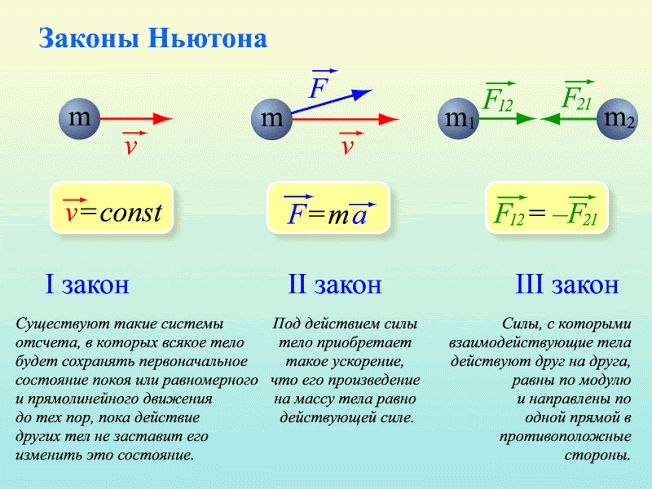
Второй Закон Ньютона связывает меру взаимодействия тел и меру инертности тела с результатом взаимодействия. Мерой взаимодействия является сила, мерой инертности – масса. Результат взаимодействия выражается в изменении скорости – ускорении. Ускорение, получаемое телом, прямо пропорционально силе, действующей на тело, и обратно пропорционально его массе.
Третий Закон Ньютона устанавливает невозможность одностороннего приложения силы. Фактически, это закон сохранения, утверждающий, что если на тело действует сила со стороны другого тела, то на другое тело действует точно такая же сила со стороны первого. Силы эти не компенсируют друг друга потому, что приложены к разным телам.
Совершая прыжок, вы сообщаете некоторую силу Земле. В результате чего Земля, согласно Третьему Закону Ньютона, также сообщает вам точно такую же силу. И вы, и Земля – приобретаете некоторые ускорения, и начинаете двигаться в разных направлениях. Поскольку масса Земли примерно в $10^{23}$ раз больше вашей массы, скорость приобретенная Землей в результате вашего прыжка, будет во столько же раз меньше.
Динамика вращения
Вращение тела заключается в том, что при движении траектории его точек являются окружностями с центрами, лежащими на одной прямой, называемой осью вращения.

То есть, путь, проходимый различными точками различен и пропорционален радиусу поворота. Поэтому динамические характеристики вращательного движения используют не величину пройденного пути, а величину угла поворота и радиус поворота. И мера взаимодействия, и мера инертности включает в себя этот радиус (расстояние от точки приложения до центра вращения).
Мера взаимодействия для вращения называется момент силы, и равна произведению величины силы на ее плечо (если сила направлена перпендикулярно радиусу, плечо равно радиусу):
$$M=F l_F$$
Мера инертности называется момент инерции, и для матеральной точки он равен произведению массы на квадрат радиуса вращения:
$$J=m R^2$$
Перемещение, скорость и сила для вращательного движения становятся угловыми – угол поворота $alpha$ радиан, угловая скорость $omega$ радиан в секунду, угловое ускорение $varepsilon$ радиан в секунду за секунду.
Таким образом, законы динамики вращения материальной точки выглядят следующим образом:
- Первый закон: $omega = const, при M=0$;
- Второй закон: $varepsilon = {M \over J}$;
- Третий закон: $M_{12}=- M_{21}$
Все три закона имеют вид, аналогичный законам для поступательного движения.

Что мы узнали?
Все три закона динамики для вращательного движения имеют вид, аналогичный законам динамики для прямолинейного движения. Но, все динамические параметры для вращения являются угловыми и включают в себя радиус вращения.








Комментирование закрыто