
Электричество и магнетизм долгое время считались мало связанными явлениями. Однако в середине XIX в. было обнаружено, что, хотя статичные электрические заряды никак не реагируют на магнитное поле, движущиеся заряды с ним взаимодействуют. Расскажем кратко о действии магнитного поля на движущийся электрический заряд.

Несмотря на правильное математическое описание, закон Ампера не раскрывает механизма возникновения силы, действующей на проводник в магнитном поле. Механизм возникновения силы Ампера был установлен только к концу XIX в., когда было доказано, что электрический ток представляет собой движение носителей заряда в проводнике, а на любой движущийся заряд со стороны магнитного поля действует сила, названная впоследствии силой Лоренца. Кратко говоря, сложение всех сил Лоренца, действующих на все заряды в проводнике, дает в итоге силу Ампера.
Сила Лоренца
Для определения действия магнитного поля на движущийся заряд можно использовать закон Ампера. Очевидно, что сила Лоренца, действующая на отдельный заряд, равна отношению силы Ампера, действующей на проводник, к количеству зарядов в этом проводнике. Из курса физики за 11 класс известно, что сила, действующая на проводник со стороны магнитного поля с индукцией $\overrightarrow B$, равна:
$$F= I |\overrightarrow B| Δl sin alpha$$
А ток в проводнике связан с зарядом $q$ и концентрацией носителей $n$ соотношением:
$$I = qnvS$$
В этой формуле $v$ — это линейная скорость движения носителей, а $S$ — площадь поперечного сечения проводника. Подставив значение тока в предыдущую формулу, получим выражение для силы Ампера:
$$F_A= |q| nvS |\overrightarrow B| Δl sin alpha$$
Число носителей заряда в проводнике равно:
$$N = nSΔl$$
Чтобы найти силу, действующую на каждый носитель (силу Лоренца), необходимо силу Ампера поделить на число носителей. В результате имеем:
$$F_Л={F_A\over N}= |q| v B sin alpha$$
Поскольку носители заряда движутся в направлении электрического тока, то угол $alpha$ равен углу между вектором скорости движения заряда и вектором магнитной индукции.
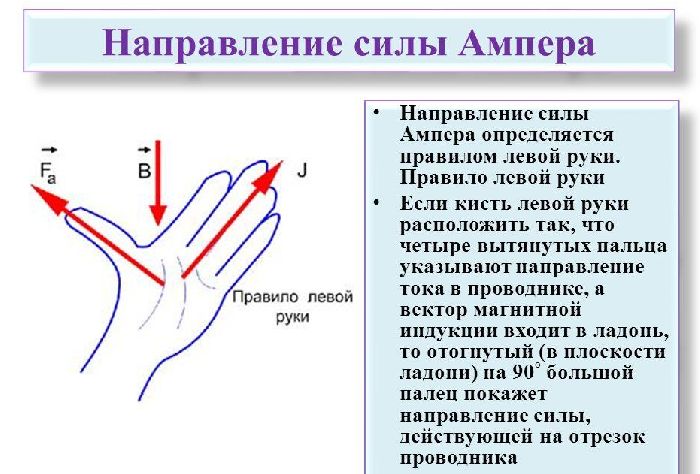
Направление силы Лоренца определяется так же, как и направление силы Ампера, по правилу левой руки. Только направление тока заменяется на направление движения положительного заряда: если четыре вытянутых пальца левой руки указывают направление движения положительного заряда, а вектор магнитной индукции прокалывает ладонь (входит в ладонь), то отставленный большой палец укажет направление силы Лоренца.
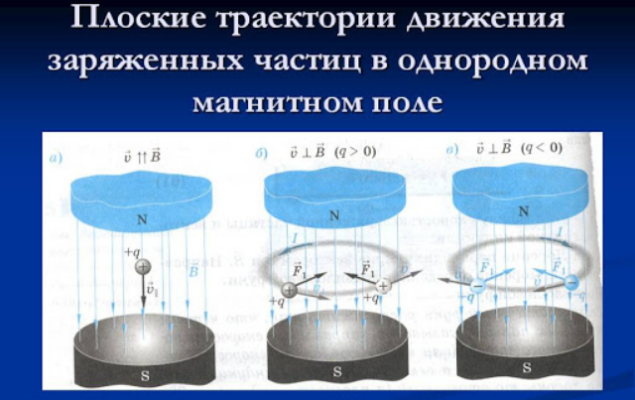
Направление силы Лоренца всегда перпендикулярно скорости, а значит, траекторией движения заряда в магнитном поле является окружность (или спираль) некоторого радиуса. Отметим также, что сила Лоренца не совершает работы и не меняет кинетическую энергию частицы. Она лишь меняет направление ее движения.
Что мы узнали?
На заряд, движущийся в магнитном поле, действует сила Лоренца. Ее направление перпендикулярно векторам скорости и магнитной индукции. Определяется оно так же, как сила Ампера: мнемоническим правилом левой руки.








Комментирование закрыто